[lwptoc numeration="none" title="目录"]
工作中有时要对照干湿球表,查露点温度什么的。研究了一下露点温度的计算方法,在python里练手感觉不错。
1、整体思路
①输入干球温度、相对湿度
②由干球温度求饱和蒸汽压( Goff-Gratch方程直接算出)
③由相对湿度求当前蒸汽压
④由当前蒸汽压倒推露点温度(牛顿迭代法倒推Goff-Gratch方程)
2、Goff-Gratch方程
由干球温度计算饱和蒸汽压的方程,被世界气象组织推荐的。准确度高但是颇为复杂。
引自:潘晓春等《大气湿球温度计算的牛顿迭代法》
另外需要留意这里温度用的是绝对温度,单位K。
python代码如下:(用到了sympy库,下面说明)
def f(x, y_0=0.0):
# Goff-Gratch方程,x=温度/K,y=饱和蒸汽压/hPa
y = pow(10,
(10.79574 * (1 - 273.16 / x)
- 5.028 * log(x / 273.16, 10.0)
+ 1.50475 * 1e-4 * (1 - pow(10, -8.2969 * (x / 273.16 - 1)))
+ 0.4287 * 1e-3 * (pow(10, 4.76955 * (1 - 273.16 / x)) - 1)
+ 0.78614
)
)
return y - y_0
其中y_0是稍后用于牛顿迭代法去逼近的y值。
3、Goff-Gratch方程的求导
牛顿迭代法需要求解函数的导数,手工算就太难了……
偷懒用sympy库的diff方法对Goff-Gratch方程求导。
python代码如下:(记得代码前加入from sympy import diff, symbols, log)
from sympy import diff, symbols, log
def df(x):
"""
原函数的导数
:param x: float类型
:return: float类型,返回df(x)。
"""
t = symbols('t', real=True) # 用于f求导的sympy.symbol类型
y = diff(f(t), t, 1) # 求f的导数,避免混淆以t做自变量
return y.evalf(subs={t: x}) # 参数x代入自变量t求值
4、牛顿迭代法
“牛顿迭代法是一种在实数域和复数域上近似求解方程的方法。”
介绍:https://zh.wikipedia.org/wiki/%E7%89%9B%E9%A1%BF%E6%B3%95
在python中构造迭代函数:
def newtonMethod(x_n, y_0, time=0):
fx_n = f(x_n, y_0=y_0) # 避免后续过程多次计算fx
dfx_n = df(x_n) # 避免后续过程多次计算dfx
print('第%s次迭代:\tx=%s,\tf(x) = %s,\tdf(x) =%s' %
(str(time), str(x_n), str(fx_n), str(dfx_n),))
if f(x_n, y_0=y_0) == 0.0: # 如果f(x)恰好为0,则完成迭代
print('解为:\tx = %s,\tf(x) = %s' % (str(x_n), str(f(x_n))))
return x_n
else:
x_n1 = x_n - fx_n / dfx_n
dx_n1 = f(x_n1, y_0=y_0)
if abs(fx_n - dx_n1) < 1e-6: # 迭代完成条件
print('解为:\tx = %s,\tf(x) = %s' %
(str(x_n1), str(dx_n1)))
return x_n1 # 精度足够,返回解x_n1
else:
return newtonMethod(x_n1, y_0, time=time + 1) # 精度未够,进入下次迭代
调用newtonMethods调用时,y_n是待逼近的饱和蒸汽压。
而x_n参数需传入一个接近露点温度的估值,这里一般用干球温度就可以了。大约4-6次就可以逼近到足够进度了。
执行:
# 传入干球温度26.0℃,26.88hPa当前蒸汽压(大约80%相对湿度) newtonMethod(26.0 + 273.15, 26.88)
结果:(295.43K = 22.28℃)
5、最终效果
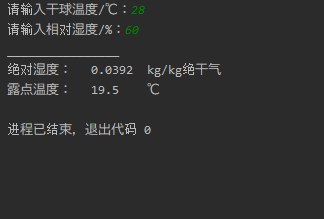
手动input干球温度和相对湿度,开始计算。
代码如下:(顺手加上了绝对湿度)
if __name__ == '__main__':
dry_bulb = float(input('请输入干球温度/℃:'))
relative_humidity = float(input('请输入相对湿度/%:'))
print('________________')
saturated_vapor_pressure = f(dry_bulb + 273.15) # 饱和蒸汽压/hPa
recent_vapor_pressure = saturated_vapor_pressure * relative_humidity / 100 # 当前蒸汽压/hPa
absolute_humidity = 0.622 * relative_humidity / (1013.25 - relative_humidity) # 绝对湿度 kg/kg绝干气。1013.25hPa是标准大气压
# 露点温度/℃,以牛顿迭代式求解(以干球温度为初始逼近值)
dew_point_temperature = newtonMethod(dry_bulb + 273.15, recent_vapor_pressure) - 273.15
print('绝对湿度:\t%s\t%s' % (round(absolute_humidity, 4), 'kg/kg绝干气'))
print('露点温度:\t%s\t%s' % (round(dew_point_temperature, 1), '℃'))
最终效果如图:
还不错。
但是……其实一般情况下用Magnus经验公式,直接解方程就够了……
试了下常用温湿度差别不超过0.1℃……
总之还不错啦。
Github:https://github.com/fatmkii/dew_point_temperature
完整代码:
from sympy import diff, symbols, log
def f(x, y_0=0.0):
"""
待求解的原函数
:param x: float类型
:param y_0: float类型。待求的x_0值,使得f(x_0)=y_0。
:return: float类型
"""
# Goff-Gratch方程,x=温度/K,y=饱和蒸汽压/hPa
y = pow(10,
(10.79574 * (1 - 273.16 / x)
- 5.028 * log(x / 273.16, 10.0)
+ 1.50475 * 1e-4 * (1 - pow(10, -8.2969 * (x / 273.16 - 1)))
+ 0.4287 * 1e-3 * (pow(10, 4.76955 * (1 - 273.16 / x)) - 1)
+ 0.78614
)
)
return y - y_0
def df(x):
"""
原函数的导数
:param x: float类型
:return: float类型,返回df(x)。
"""
t = symbols('t', real=True) # 用于f求导的sympy.symbol类型
y = diff(f(t), t, 1) # 求f的导数,避免混淆以t做自变量
return y.evalf(subs={t: x}) # 参数x代入自变量t求值
def newtonMethod(x_n, y_0, time=0):
"""
牛顿迭代法
:param x_n: float类型,本次迭代的x
:param y_0: float类型,使f(x_n)值尽可能逼近y_0
:param time: int类型,迭代次数显示
:return: 迭代退出后返回x_n,使得f(x_n)=y_0
"""
fx_n = f(x_n, y_0=y_0) # 避免后续过程多次计算fx
dfx_n = df(x_n) # 避免后续过程多次计算dfx
# print('第%s次迭代:\tx=%s,\tf(x) = %s,\tdf(x) =%s' %
# (str(time), str(x_n), str(fx_n), str(dfx_n),))
if f(x_n, y_0=y_0) == 0.0: # 如果f(x)恰好为0,则完成迭代
# print('解为:\tx = %s,\tf(x) = %s' % (str(x_n), str(f(x_n))))
return x_n
else:
x_n1 = x_n - fx_n / dfx_n
dx_n1 = f(x_n1, y_0=y_0)
if abs(fx_n - dx_n1) < 1e-6: # 迭代完成条件
# print('解为:\tx = %s,\tf(x) = %s' %
# (str(x_n1), str(dx_n1)))
return x_n1 # 精度足够,返回解x_n1
else:
return newtonMethod(x_n1, y_0, time=time + 1) # 精度未够,进入下次迭代
if __name__ == '__main__':
dry_bulb = float(input('请输入干球温度/℃:'))
relative_humidity = float(input('请输入相对湿度/%:'))
print('________________')
saturated_vapor_pressure = f(dry_bulb + 273.15) # 饱和蒸汽压/hPa
recent_vapor_pressure = saturated_vapor_pressure * relative_humidity / 100 # 当前蒸汽压/hPa
absolute_humidity = 0.622 * relative_humidity / (1013.25 - relative_humidity) # 绝对湿度 kg/kg绝干气。1013.25hPa是标准大气压
# 露点温度/℃,以牛顿迭代式求解(以干球温度为初始逼近值)
dew_point_temperature = newtonMethod(dry_bulb + 273.15, recent_vapor_pressure) - 273.15
print('绝对湿度:\t%s\t%s' % (round(absolute_humidity, 4), 'kg/kg绝干气'))
print('露点温度:\t%s\t%s' % (round(dew_point_temperature, 1), '℃'))